Slow forward scattering. More...
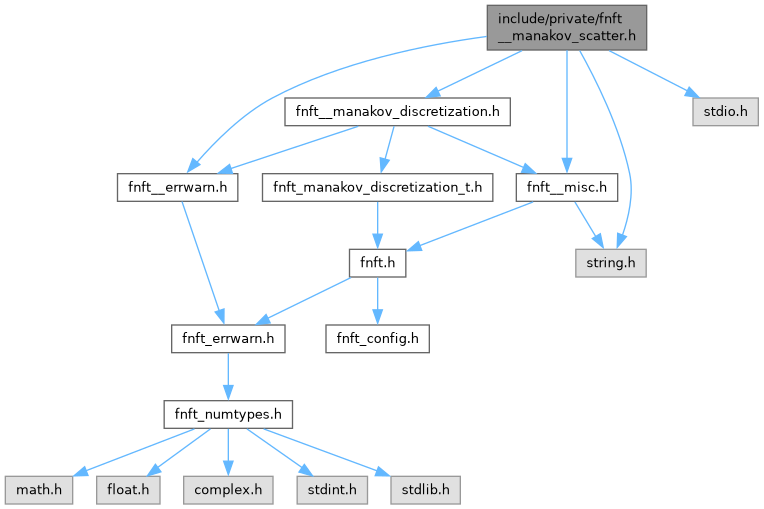
#include "fnft__manakov_discretization.h"#include <stdio.h>#include <string.h>#include "fnft__errwarn.h"#include "fnft__misc.h"
Include dependency graph for fnft__manakov_scatter.h:
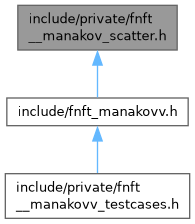
This graph shows which files directly or indirectly include this file:
Go to the source code of this file.
Functions | |
| FNFT_INT | fnft__manakov_scatter_matrix (FNFT_UINT const D, FNFT_COMPLEX const *const q1, FNFT_COMPLEX const *const q2, FNFT_REAL const eps_t, FNFT_UINT const K, FNFT_COMPLEX const *const lambda, FNFT_INT const kappa, FNFT_COMPLEX *const result, fnft_manakov_discretization_t const discretization) |
| Computes the scattering matrix. | |
Detailed Description
Slow forward scattering.
Function Documentation
◆ fnft__manakov_scatter_matrix()
| FNFT_INT fnft__manakov_scatter_matrix | ( | FNFT_UINT const | D, |
| FNFT_COMPLEX const *const | q1, | ||
| FNFT_COMPLEX const *const | q2, | ||
| FNFT_REAL const | eps_t, | ||
| FNFT_UINT const | K, | ||
| FNFT_COMPLEX const *const | lambda, | ||
| FNFT_INT const | kappa, | ||
| FNFT_COMPLEX *const | result, | ||
| fnft_manakov_discretization_t const | discretization | ||
| ) |
Computes the scattering matrix.
The function computes the scattering matrix with respect to \(\lambda\). The bo method is based on the paper by Boffetta and Osborne (J. Comput. Physics 1992 ). The CF4_2 method is based on the article by Chimmalgo, Prins and Wahls (IEEE 2018 ).
- Parameters
-
[in] D Number of samples [in] q1 Array of length D, contains samples of the first element of the potential function \( q1_n\) for \(n=0,1,\dots,D-1\) in ascending order (i.e., \( q1_0, q1_1, \dots, q1_{D-1} \)). [in] q2 Array of length D, contains samples of the first element of the potential function \( q2_n\) for \(n=0,1,\dots,D-1\) in ascending order (i.e., \( q2_0, q2_1, \dots, q2_{D-1} \)). [in] eps_t timestep size [in] K Number of values of \(\lambda\). [in] lambda Array with values of \(\lambda\). [in] kappa dispersion constant. kappa=-1 for normal dispersion, kappa=+1 for anomalous dispersion [out] result Array of length 9*K containing S=[S11(lambda[0]) S12(lambda[0]) S13(lambda[0]) ... S33(lambda[K-1])] upon exit where S = [S11, S12, S13; S21, S22, S23; S31, S32, S33] is the scattering matrix computes using the chosen discretization [in] discretization Discretization to be used. Should be of type fnft_manakov_discretization_t. Check fnft_manakov_discretization_t to see which discretizations correspond to slow methods