fnft__manakov_fscatter.h File Reference

Computes the polynomial approximation of the combined scattering matrix. More...

#include "fnft__manakov_discretization.h"
#include "fnft__misc.h"
#include "fnft__errwarn.h"
#include "fnft__poly_fmult.h"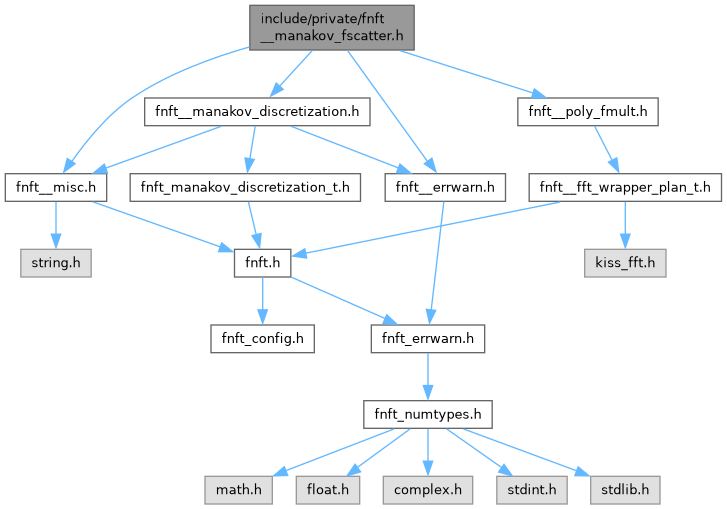

Include dependency graph for fnft__manakov_fscatter.h:

This graph shows which files directly or indirectly include this file:

Go to the source code of this file.

Functions
FNFT_UINT	fnft__manakov_fscatter_numel (FNFT_UINT D, fnft_manakov_discretization_t discretization)
	Returns the length of transfer_matrix to be allocated based on the number of samples and discretization.
FNFT_INT	fnft__manakov_fscatter (const UINT D, COMPLEX const *const q1, COMPLEX const *const q2, const INT kappa, REAL eps_t, COMPLEX *const result, UINT *const deg_ptr, INT *const W_ptr, manakov_discretization_t const discretization)
	Fast computation of polynomial approximation of the combined scattering matrix.

Detailed Description

Computes the polynomial approximation of the combined scattering matrix.

Function Documentation

fnft__manakov_fscatter()

FNFT_INT fnft__manakov_fscatter	(	const UINT	D,
		COMPLEX const *const	q1,
		COMPLEX const *const	q2,
		const INT	kappa,
		REAL	eps_t,
		COMPLEX *const	result,
		UINT *const	deg_ptr,
		INT *const	W_ptr,
		manakov_discretization_t const	discretization
	)

Fast computation of polynomial approximation of the combined scattering matrix.

This routine computes the polynomial approximation of the combined scattering matrix by multipying together individual scattering matrices.
Individual scattering matrices depend on the chosen discretization.
The main reference is Wahls and Poor (Proc. ICASSP 2013 ).

Parameters

[in]	D	Number of samples
[in]	q1	Array of length D, contains samples \( q1(t_n)=q1(x_0, t_n) \), where \( t_n = T[0] + n(T[1]-T[0])/(D-1) \) and \(n=0,1,\dots,D-1\), of the to-be-transformed signal in ascending order (i.e., \( q1(t_0), q1(t_1), \dots, q1(t_{D-1}) \))
[in]	q2	Same as q1, but for the second element of the potential function
[in]	kappa	Dispersion constant. kappa=+1 for normal dispersion and kappa=-1 for anomalous dispersion
[in]	eps_t	Step-size, eps_t \(= (T[1]-T[0])/(D-1) \).
[out]	result	array of length manakov_fscatter_numel(D,discretization), will contain the combined scattering matrix. Result needs to be pre-allocated with malloc(manakov_fscatter_numel(D,discretization)*sizeof(COMPLEX)).
[out]	deg_ptr	Pointer to variable containing degree of the discretization. Determined based on discretization by fnft__manakov_discretization_degree.
[out]	W_ptr	Pointer to normalization flag fnft_manakovv_opts_t::normalization_flag.
[in]	discretization	The type of discretization to be used. Should be of type fnft_nse_discretization_t. Not all fnft_manakov_discretization_t discretizations are supported. Check fnft_manakov_discretization_t for list of supported types.

Returns

FNFT_SUCCESS or one of the FNFT_EC_... error codes defined in fnft_errwarn.h.

fnft__manakov_fscatter_numel()

FNFT_UINT fnft__manakov_fscatter_numel	(	FNFT_UINT	D,
		fnft_manakov_discretization_t	discretization
	)

Returns the length of transfer_matrix to be allocated based on the number of samples and discretization.

This routine returns the length 9*misc_nextpowerof2(D)*(manakov_discretization_degree(discretization) + 1) to be allocated based on the number of samples and discretization of type discretization.

Parameters

[in]	D	Number of samples.
[in]	discretization	Type of discretization from fnft_manakov_discretization_t.

Returns

Returns the length to be allocated. Returns 0 for unknown discretizations.